The position of the boat heading east at time t is

Since we take b to b the distance the second boat is south of the initial position and the boat is. The distance travelled by the spaceship between t 0 and t T.

Two boats leave port at the same time.

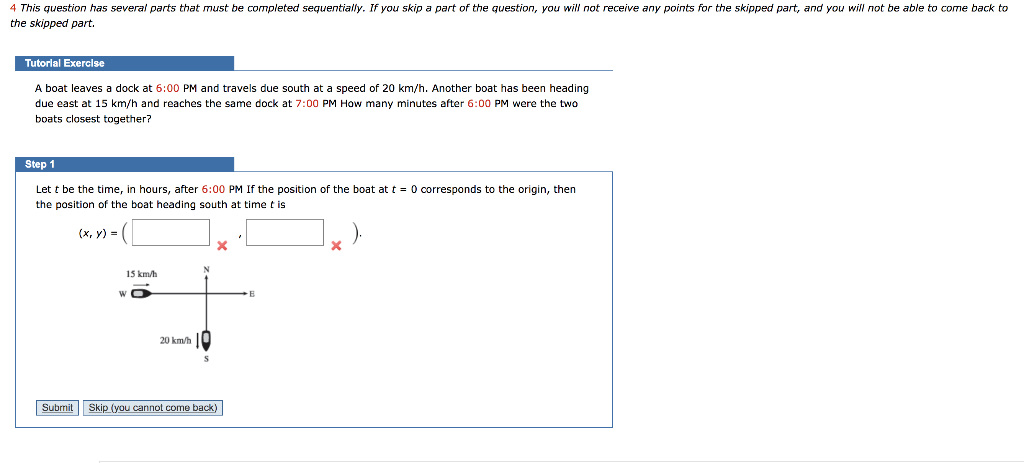
The position of the boat heading east at time t is. Step 1 Lett be the time in hours after 800 PM If the position of the boat at t 0 corresponds to the origin then the position of the boat heading south at time t is x y 0 - 20t 20t 15 kmh w E 20 kmh Step 2 The position of the boat heading east at time t is xy -15 -15 15t O ol. Start over- because we take a to be the distance the first boat is east of the initial position and the boat is going east at constant speed 15 kmhr then a 15t. Since we take b to b the distance the second boat is south of the initial position and the boat is.

At time t O. A second boat B is at the point with position vector Given that the velocity of B is 3i 4j m s- c show that A and B will collide at a point P and find the position vector of P. 5 Given instead that B has speed 8 m s.

I and moves in the direction of the vector 3i. A boats speed in still water is v BW 185 ms. If the boat is to travel directly across a river whose current has speed v WS 120 ms at what upstream angle must the boat head.

X y q 40 4 1 85 1 20 0 1 1. Sin v v sin v v sin v sin v x BW WS BW WS BW WS T T T - component. The x-component of v BW cancels.

A boat leaves the dock at t 0 and heads out into a lake with an acceleration of 20 m s 2 i. 20 m s 2 i. A strong wind is pushing the boat giving it an additional velocity of 20 ms i 10 ms j.

20 ms i 10 ms j. A What is the velocity of the boat at t 10 s. B What is the position of the boat at t 10s.

The position function r t rt gives the position as a function of time of a particle moving in two or three dimensions. Graphically it is a vector from the origin of a chosen coordinate system to the point where the particle is located at a specific time. A ball is thrown eastward into the air from the origin in the direction of the positive x-axis.

The initial velocity is 50 i 80 k with speed measured in feet per second. The spin of the ball results in a southward acceleration of 4 f t s 2 so the acceleration vector is a 4 j 32 k. Solved for t t 2 xf-xi ViVf t 2 11m-00m 27ms 17ms t 50 seconds.

A boat is cruising in a straight line at a constant speed of 27 ms when it is shifted into neutral. After coasting 11 m the engine is engaged again and the boat resumes cruising at the reduced constant speed of 17 ms. VesselFinder is a FREE AIS vessel tracking web site.

VesselFinder displays real time ship positions and marine traffic detected by global AIS network. Step 1 Let t be the time in hours after 800 PM If the position of the boat att 0 corresponds to the origin then the position of the boat heading south at time t is x y 0 -20t -20t 15 kmh wO E 20 kmh Step 2 The position of the boat heading east at time t is x y -15 -1515t 0 Step 3 The distance D between the two boats is given by x t 12 20 D V-15. A model boat A moves on a lake with constant velocity i 6j m s-1.

At time t 0 A is at the point with position vector 2i 1 Oj m. Find a the speed of A 2 b the direction in which A is moving giving your answer as a bearing. 3 At time t 0 a second boat B IS at the point with position vector 26i 4j m.

A boat on the southern shore wants to reach a port on the northern shore which is located 08km away from the boats initial position at an angle of 60 degrees. Two boats leave port at the same time. The first boat travels due east 90 degrees at 14 mph and the second travels at 28 mph in the direction N30 degrees east.

Two boats leave. Finding velocity at time t Therefore if an object say a boat is at position vector -4i 3jkm and is moving at a speed of 4i 17jkmh-1 then after time t its new position will be. Initial position displacement Postion vΔt -4i 3jkm 4i 17jt.

While the boat heads towards the opposite shore it is the current which provides the power to carry the boat parallel to the rivers banks. The current carries the boat down the river. And the distance which the boat is carried down the river is dependent upon the time of travel and the speed of the current.

Motion does not happen in isolation. If youre riding in a train moving at 10 ms east this velocity is measured relative to the ground on which youre traveling. However if another train passes you at 15 ms east your velocity relative to this other train is different from your velocity relative to the ground.

This angle can be determined using a trigonometric function as shown below. Tan theta oppositeadjacent tan theta 34 theta invtan 34 theta 369 degrees. Given a boat velocity of 4 ms East and a river velocity of 3 ms North the resultant velocity of the boat will be.

The vector equation is v PG v PAv AG v PG v PA v AG where P plane A air and G ground. From the geometry in Figure we can solve easily for the magnitude of the velocity of the plane with respect to the ground and the angle of the planes heading θ. Heading and track A to B 1 True North 2 Heading the direction the vessel is pointing towards 3 Magnetic north which differs from true north by the magnetic variation.

4 Compass north including a two-part error. The magnetic variation 6 and the ships own magnetic field 5. A boat is heading due north as it crosses a wide river with a velocity of 10kmhr relative to the waterthe river has a velocity of 5km due east determine the velocity of the boat with respect on the river bank.

A boat travels at 38 ms and heads straight across a. The graph below shows the variation with time t of the acceleration a of a spaceship. A 0 0 T t The spaceship is at rest at t 0.

The shaded area represents A. The distance travelled by the spaceship between t 0 and t T. The speed of the spaceship at t T.

The rate at which the speed of the spaceship changes between t 0 and t T. The rate at which the acceleration. If the boat departs from position X heading due north in what direction will this boat travel relative to position X.

35 o E of N c. 43 o E of N d. 47 o E of N 22.

Which one of the following contains two vector quantities. In addition to obtaining the displacement and velocity vectors of an object in motion we often want to know its acceleration vector at any point in time along its trajectory. This acceleration vector is the instantaneous acceleration and it can be obtained from the derivative with respect to time of the velocity function as we have seen in a previous chapter.

Under certain circumstances such as low visibility only one line of position can be obtained at a time. In this event a line of position obtained at an earlier time may be advanced to the time of the later LOP. These two LOPs should not be parallel to each other.

Remember that the optimal angular spread is 90.